7. Summarizing model outputs
Learning Objectives and Outline
Learning Objectives
Be able to derive summary outcomes (costs and health outcomes) from a Markov trace
Be able to apply methods for:
Cycle correction
Discounting a stream of costs (or benefits) and calculating net present value
Adjusting costs measured in different currencies to a common currency (and currency year)
Outline
- Calculating Life Years
- Cycle correction
- Inflation Adjustment
- Currency Conversion
- Discounting
- Calculating Total Costs and QALYs
Calculating Life Years
A Markov trace from Case Study 2…
| Cycle | Healthy | Sick | Dead |
|---|---|---|---|
| 0 | 1.000 | 0.000 | 0.000 |
| 1 | 0.856 | 0.138 | 0.007 |
| 2 | 0.732 | 0.253 | 0.015 |
| 3 | 0.626 | 0.349 | 0.025 |
| 4 | 0.536 | 0.429 | 0.035 |
| 5 | 0.458 | 0.495 | 0.046 |
| … | … | … | … |
| 75 (End) | 0 | 0.282 | 0.718 |
Life years
Life years = cumulative “reward” of being in an “alive” (healthy or sick) state
| Cycle | Healthy | Sick | Dead | LY (single cycle) |
|---|---|---|---|---|
| 0 | 1.000 | 0.000 | 0.000 | 1 |
| 1 | 0.856 | 0.138 | 0.007 | 0.856 + 0.138 = 0.993 |
| 2 | 0.732 | 0.253 | 0.015 | 0.732 + 0.253 = 0.985 |
| 3 | 0.626 | 0.349 | 0.025 | 0.975 |
| 4 | 0.536 | 0.429 | 0.035 | 0.965 |
| 5 | 0.458 | 0.495 | 0.046 | 0.954 |
| … | … | … | … | |
| 75 (End) | 0 | 0.282 | 0.718 | 0.282 |
Life years
| Cycle | Healthy | Sick | Dead | LY (single cycle) | LY (cumulative) |
|---|---|---|---|---|---|
| 0 | 1.000 | 0.000 | 0.000 | 1 | 1 |
| 1 | 0.856 | 0.138 | 0.007 | 0.993 | 1 + 0.993 = 1.993 |
| 2 | 0.732 | 0.253 | 0.015 | 0.985 | |
| 3 | 0.626 | 0.349 | 0.025 | 0.975 | |
| 4 | 0.536 | 0.429 | 0.035 | 0.965 | |
| 5 | 0.458 | 0.495 | 0.046 | 0.954 | |
| … | … | … | … | … | |
| 75 (End) | 0 | 0.282 | 0.718 | 0.282 |
Life years
| Cycle | Healthy | Sick | Dead | LY (single cycle) | LY (cumulative) |
|---|---|---|---|---|---|
| 0 | 1.000 | 0.000 | 0.000 | 1 | 1 |
| 1 | 0.856 | 0.138 | 0.007 | 0.993 | 1.993 |
| 2 | 0.732 | 0.253 | 0.015 | 0.985 | 1 + 0.993 + 0.985 = 2.978 |
| 3 | 0.626 | 0.349 | 0.025 | 0.975 | |
| 4 | 0.536 | 0.429 | 0.035 | 0.965 | |
| 5 | 0.458 | 0.495 | 0.046 | 0.954 | |
| … | … | … | … | … | |
| 75 (End) | 0 | 0.282 | 0.718 | 0.282 |
Life years
| Cycle | Healthy | Sick | Dead | LY (single cycle) | LY (cumulative) |
|---|---|---|---|---|---|
| 0 | 1.000 | 0.000 | 0.000 | 1 | 1 |
| 1 | 0.856 | 0.138 | 0.007 | 0.993 | 1.993 |
| 2 | 0.732 | 0.253 | 0.015 | 0.985 | 2.978 |
| 3 | 0.626 | 0.349 | 0.025 | 0.975 | 3.954 |
| 4 | 0.536 | 0.429 | 0.035 | 0.965 | 4.919 |
| 5 | 0.458 | 0.495 | 0.046 | 0.954 | 5.872 |
| … | … | … | … | … | … |
| 75 (End) | 0 | 0.282 | 0.718 | 0.282 | 44.825 |
The cumulative LYs for an individual starting in the Healthy state is 44.825
Note that this is within a 75 years time horizon
- They may still be alive and keep accumulating LYs if we extend the time horizon
Cycle correction
The problem
- Time is continuous, so are survival/event-free survival curves
- When we discretize time by using a fixed cycle length, we can make two assumptions
- Suppose this is a simple Well → Dead process
The problem
Assuming death happens at the end of cycle (A)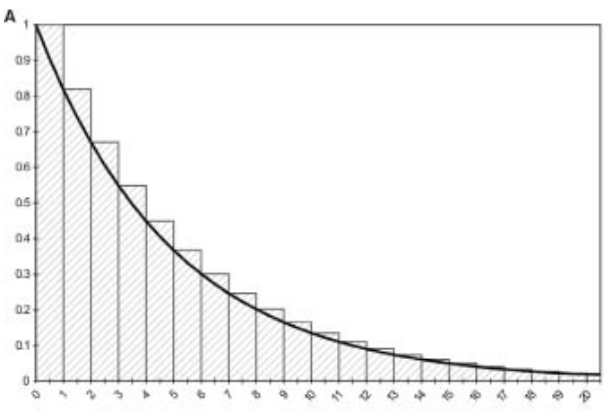
Overestimates state membership in Well
Assuming death happens at the start of cycle (B)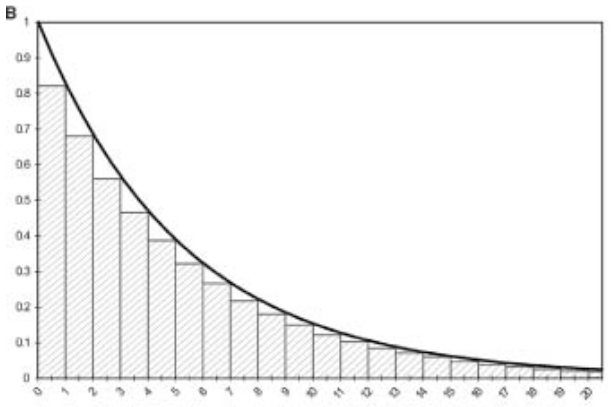
Underestimates state membership in Well
Methods to address this problem
Half-cycle correction
Simpson’s 1/3 correction
Half-cycle correction
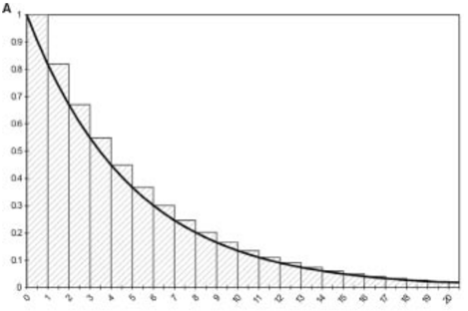
Half-cycle correction
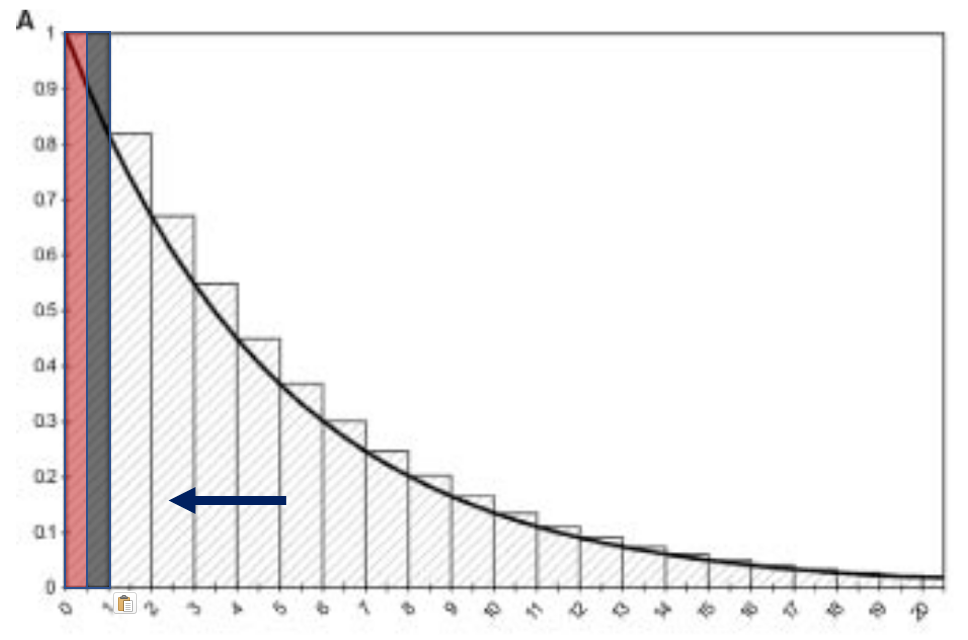
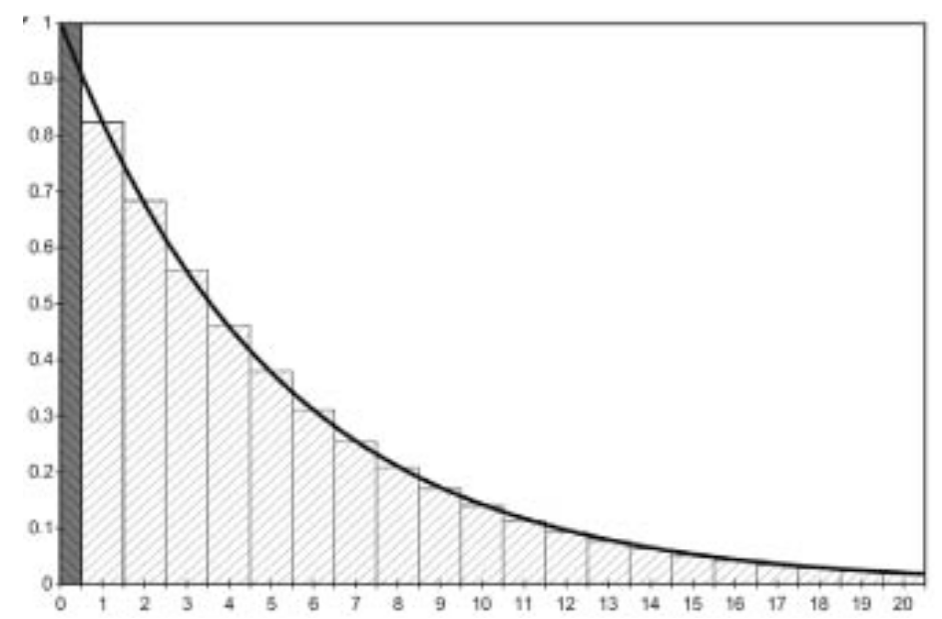
Half-cycle correction
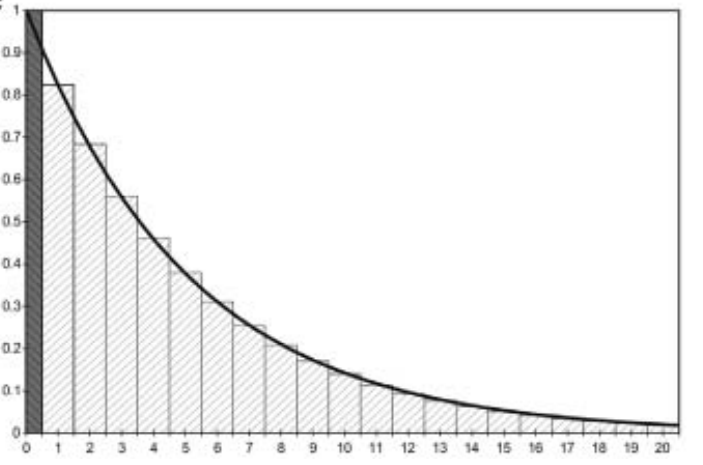
Multiply the outcomes by 1/2 in the first and last cycle.
Shifting the computed, discrete state membership curve to the left by 1/2 cycle.
Essentially assuming that events happen in the middle of cycle
Half-cycle correction
It can still be imprecise, especially when there’s more curvature in the true, continuous curve:
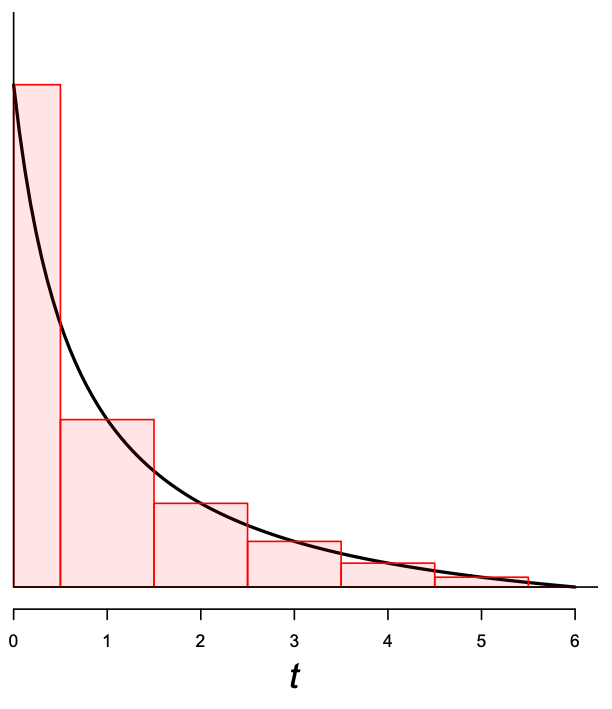
Simpson’s 1/3 Correction
- Uses the area under the quadratic curve passing through 3 points {tk−1,tk,tk+1}
- Multiply the outcomes by 1/3 in the first and last cycle.
- Multiply the outcomes by 4/3 if the cycle number is odd and by 2/3 if the cycle number is even.
- Note that the time horizon must be even ← This formation requires 2 sub-intervals from tk−1 to tk+1
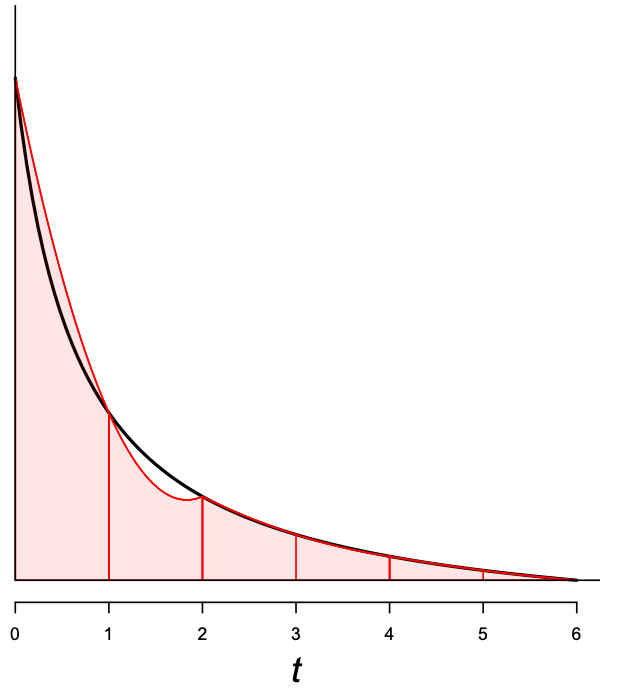
Comparison of Methods: Summary
Standard half-cycle correction is the most widely used approach
Simpson’s 1/3 method performs the best among existing methods (It converges to the continuous-time exact solutions the fastest)
The choice of method matters less with shorter cycle length
To learn more: Elbasha EH, Chhatwal J. Theoretical Foundations and Practical Applications of Within-Cycle Correction Methods. Med Decis Making. 2016 Jan 1;36(1):115–31.
Apply cycle correction methods to our CS2 markov trace…
Half-cycle correction
- Multiply the outcomes by 1/2 in the first and last cycle.
| Cycle | Healthy | Sick | Dead | LY (single cycle, adjusted) | LY (cumulative) |
|---|---|---|---|---|---|
| 0 | 1.000 | 0.000 | 0.000 | 1*0.5 | 0.5 |
| 1 | 0.856 | 0.138 | 0.007 | 0.993 | 0.5 + 0.993 = 1.493 |
| 2 | 0.732 | 0.253 | 0.015 | 0.985 | 2.478 |
| 3 | 0.626 | 0.349 | 0.025 | 0.975 | 3.454 |
| 4 | 0.536 | 0.429 | 0.035 | 0.965 | 4.419 |
| 5 | 0.458 | 0.495 | 0.046 | 0.954 | 5.372 |
| … | … | … | … | … | … |
| 75 (End) | 0 | 0.282 | 0.718 | 0.282 *0.5 | 44.184 |
This number is smaller than our original estimate without half-cycle correction (44.825!)
Simpson’s 1/3
- Multiply the outcomes by 1/3 in the first and last cycle.
- Multiply the outcomes by 4/3 if the cycle number is odd and by 2/3 if the cycle number is even.
- Note that the time horizon must be even.
| Cycle | Healthy | Sick | Dead | LY (single cycle | Cycle Adjustment | LY (single-cycle, adjusted) | LY (cumulative) |
|---|---|---|---|---|---|---|---|
| 0 | 1.000 | 0.000 | 0.000 | 1 | 0.333 | 1*0.333 = 0.333 | 0.333 |
| 1 | 0.856 | 0.138 | 0.007 | 0.993 | 1.333 | 0.993*1.333 = 1.324 | 1.657 |
| 2 | 0.732 | 0.253 | 0.015 | 0.985 | 0.667 | 0.985*0.667 = 0.657 | 2.314 |
| 3 | 0.626 | 0.349 | 0.025 | 0.975 | 1.333 | … | … |
| 4 | 0.536 | 0.429 | 0.035 | 0.965 | 0.667 | … | … |
| 5 | 0.458 | 0.495 | 0.046 | 0.954 | 1.333 | … | … |
| … | … | … | … | … | … | … | … |
| 75 | 0 | 0.282 | 0.718 | 0.282 | 1.333 | 0.282*1.333 = 0.376 | … |
| 76 (End) | 0 | 0.277 | 0.723 | 0.277 | 0.333 | 0.277*0.333 = 0.092 | 44.454 |
Introducing some other adjustments before we get to calculating costs and QALYs…
Inflation adjustment (cost)
Currency conversion (cost)
Discounting (both cost and health)
Inflation Adjustment
Inflation Adjustment: Motivation
$100 in 2000 is not equivalent to $100 in 2020
- $100 could buy a lot more in 2000!
Important to adjust for the price difference over time, especially when working with cost sources from multiple years
Inflation Adjustment: Method
Choose a reference year (usually the current year of analysis)
Convert all costs to the reference year
Converting cost in Year X to Year Y (reference year):
Cost(Year Y)=Cost(Year X)×Price index(Year Y)Price index(Year X)
Inflation Adjustment: Example
Cost of hospitalization for mild stroke in the US was ~15,000 USD in 2013. What if we want to convert this number to 2020 USD?
CPI (Consumer Price Index) in 2013: 233
CPI in 2020: 259 (Source: US Bureau of Labor Statistics)
Cost(2020)=Cost(2013)×CPI(2020)CPI(2013)=15,000×259233=16,674 (2020 USD)
Currency Conversion
Isn’t required for CEA but may be useful in some situations:
- Example: may need to convert local currency to USD because cost-effectiveness thresholds are often estimated in the unit of USD per DALY.
Taking the capstone Rotavirus example, how do we convert 100 Indian Rupees to USD?
Current exchange rate in 2022: 1 Indian Rupee = ~0.12 USD
100 Indian Rupees = 12 USD
Discounting
Why discounting?
Adjust costs at social discount rate to reflect social “rate of time preference”
Pure time preference (“inpatience”)
Potential catastrophic risk in the future
Economic growth
How do we discount?
Present value: PV=FV/(1+r)t
FV = future value, the nominal cost incurred in the future
r = annual discount rate (analogous to interest rate)
t = number of years in future when cost is incurred
Reasonable consensus around 3% per year
May vary according to country guidelines
Adjust for inflation and currency first, then discount
Intuition
r=0.03
Recall that PV=FV/(1+r)t, and we’re at Year 0:
$1 in Year 0 is valued as 1/1.030=$1
$1 in Year 1 is valued as 1/1.031=$0.97
$1 in Year 2 is valued as 1/1.032=$0.94
$1 in Year 3 is valued as 1/1.033=$0.92
…
Example
- Assume in year 5, a patient develops disease, and there is a treatment cost of $500
- This is the future value (FV) of the cost!
- Present value PV = PV=FV/(1+r)t=500/(1+0.03)5=$431.3
Discounting health benefits
The consensus is that health benefits should be discounted at the same rate as costs
- May vary in some country guidelines
Why?
The Keeler-Cretin Paradox

The Keeler-Cretin Paradox
Imagine that an intervention would cost $100,000 and yield a 1 QALY benefit. If we discount costs at 3% per year but don’t discount QALYs…
If implementing this intervention in year 0…
| Year 0 | |
|---|---|
| Cost ($) | 100,000 |
| Health Benefit (QALY) | 1 |
| ICER ($/QALY) | 100,000 |
The Keeler-Cretin Paradox
Imagine that an intervention would cost $100,000 and yield a 1 QALY benefit. If we discount costs at 3% per year but don’t discount QALYs…
If implementing this intervention in year 1…
| Year 0 | Year 1 | |
|---|---|---|
| Cost ($) | 100,000 | 100,000/1.03 = 97,087 |
| Health Benefit (QALY) | 1 | 1 |
| ICER ($/QALY) | 100,000 | 97,087 |
The Keeler-Cretin Paradox
Imagine that an intervention would cost $100,000 and yield a 1 QALY benefit. If we discount costs at 3% per year but don’t discount QALYs…
If implementing this intervention in year 2…
| Year 0 | Year 1 | Year 2 | |
|---|---|---|---|
| Cost ($) | 100,000 | 100,000/1.03 = 97,087 | 100,000/(1.03^2) = 94,260 |
| Health Benefit (QALY) | 1 | 1 | 1 |
| ICER ($/QALY) | 100,000 | 97,087 | 94,260 |
This is where the paradox arises: It seems more favorable to indefinitely delay the intervention!
Discounting rates – Cross-country comparison
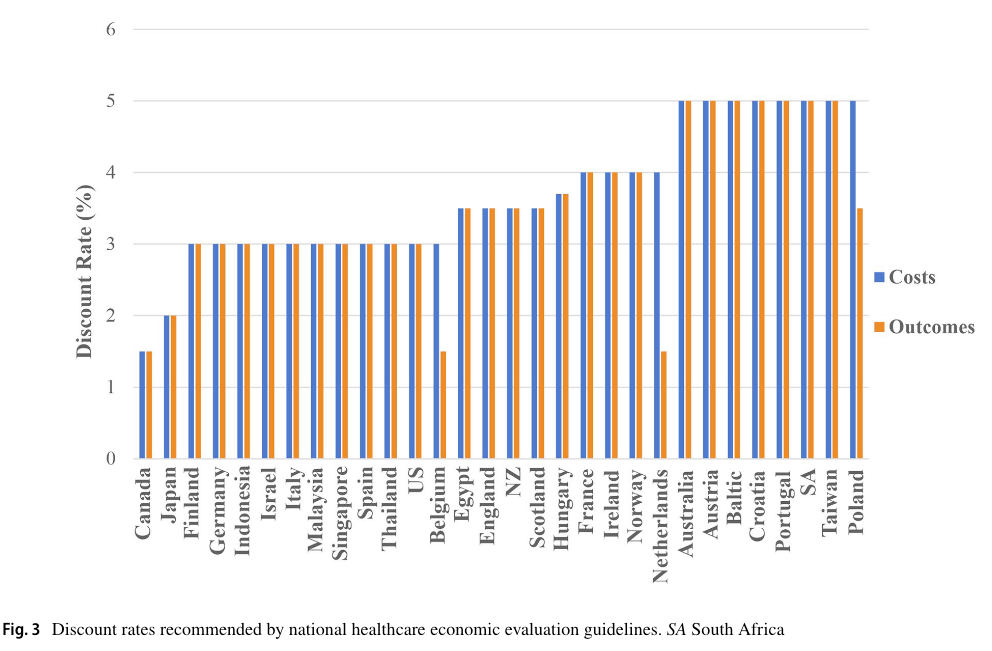
Calculating Costs and QALYs
Calculating Costs and QALYs
Costs and QALYs can be accumulated similarly as “rewards” separately
Costs:
(Transform all costs into the same currency and currency year before entering them into the model)
Cycle correction
Discounting
QALYs:
Utility weight
Cycle correction
Discounting
Calculating Costs and QALYs
We will practice how to perform all adjustments simultaneously to calculate total costs and QALYs from a Markov trace in Case Study 4!